Abstract
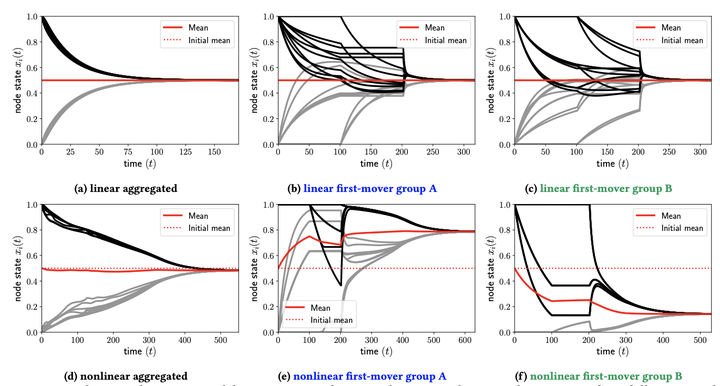
We investigate consensus dynamics on temporal hypergraphs that encode network systems with time-dependent, multi-way interactions. We compare this dynamics with that on appropriate projections of this higher-order network representation that flatten the temporal, the multi-way component, or both. For linear average consensus dynamics, we find that the convergence of a randomly switching time-varying system with multi-way interactions is slower than the convergence of the corresponding system with pairwise interactions, which in turn exhibits a slower convergence rate than a consensus dynamics on the corresponding static network. We then consider a nonlinear consensus dynamics model in the temporal setting. Here we find that in addition to an effect on the convergence speed, the final consensus value of the temporal system can differ strongly from the consensus on the aggregated, static hypergraph. In particular we observe a first-mover advantage in the consensus formation process. If there is a local majority opinion in the hyperedges that are active early on, the majority in these first-mover groups has a higher influence on the final consensus value. This is a behaviour that is not observable in this form in projections of the temporal hypergraph.
Leonie Neuhäuser
PhD Candidate in Computer Science
My research interests include Network Science, Complex Systems and Computational Social Sciences.