Abstract
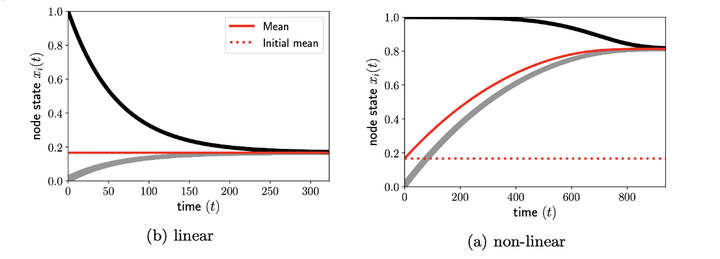
We introduce and analyse a three-body consensus model (3CM) for non-linear consensus dynamics on hypergraphs. Our model incorporates reinforcing group effects, which can cause shifts in the average state of the system even in if the underlying graph is complete (corresponding to a mean-field interaction), a phenomena that may be interpreted as a type of peer pressure. We further demonstrate that for systems with two clustered groups, already a small asymmetry in our dynamics can lead to the opinion of one group becoming clearly dominant. We show that the nonlinearity in the model is the essential ingredient to make such group dynamics appear, and demonstrate how our system can otherwise be written as a linear, pairwise interaction system on a rescaled network.
Leonie Neuhäuser
PhD Candidate in Computer Science
My research interests include Network Science, Complex Systems and Computational Social Sciences.